Terdapat beberapa distribusi statistik yang memainkan peranan penting di dalam ilmu telekomunikasi. Di antara distribusi-distribusi ini adalah distribusi binomial, distribusi Poisson, dan distribusi normal atau Gaussian.
Distribusi Binomial
Sebuah r.v X akan disebut sebagai r.v binomial dengan parameter (n,p) jika pmf-nya ditentukan melalui rumusan berikut :
[latex]p_{x}(k)=P(X=k)=\begin{pmatrix} n\\ k \end{pmatrix}p^{k}(1-p)^{n-k} \ \ \ \ \ \ k=0,1,…,n[/latex]
dimana [latex]0\leqslant p\leqslant 1[/latex] dan
[latex]\begin{pmatrix} n\\ k \end{pmatrix}=\frac{n!}{k!(n-k)!}[/latex]
yang mana besaran ini dinamakan koefisien binomial. Fungsi distribusi (cdf) dari r.v binomial X dengan demikian adalah :
[latex]F_{x}(x)=\sum_{k=1}^{m} \begin{pmatrix} n\\ k \end{pmatrix}p^{k}(1-p)^{n-k} \ \ \ \ \ m\leq x\leq m+1[/latex]
Rata-rata dan varians dari r.v binomial X adalah
[latex]\mu _{x}=np \ \ \ dan \ \ \ \ \sigma _{X}^{2}=np(1-p)[/latex]
Variabel acak binomial X adalah sebuah variabel acak diskrit yang bernilai bulat dan terkait dengan pengulangan-pengulangan sebuah eksperimen. Umpamakan bahwa kita melakukan sebuah eksperimen dan kita hendak mengamati kemunculan kejadian A saja. Apabila A muncul, maka kita mengatakan bahwa eksperimen kita berhasil, namun jika A tidak muncul ([latex]\bar{A}[/latex] muncul), maka eksperimen kita dikatakan gagal. Misalkan bahwa peluang munculnya A adalah P(A)=p, maka [latex]P(\bar{A})=q=1-p[/latex] . Kita mengulangi eksperimen kita sebanyak n kali (n percobaan) dengan berpegang pada asumsi-asumsi berikut :
1. P(A) bernilai tetap (konstan) di setiap percobaan
2. Masing-masing dari n percobaan yang dilakukan tidak bergantung pada satu sama lainnya (berdiri sendiri)
Sebuah titiak sampel (hasil) di dalam ruang sampel eksperimen ini akan terdiri dari sejumlah A dan sejumlah [latex]\bar{A}[/latex]. Sebuah titik sampel yang terdiri dari k buah A dan (n-k) buah [latex]\bar{A}[/latex]
akan memiliki peluang kemunculan sebesar [latex]p^{k}q^{n-k}[/latex], sehingga, jika X adalah sebuah variabel acak yang merepresentasikan jumlah kemunculan kejadian A di dalam n kali percobaan (atau pengulangan sebuah eksperimen), maka nilai X adalah bilangan-bilangan bulat k=0,1,..,n. Didalam ilmu telekomunikasi, distribusi binomial dapat dijumpai pada studi sistem transmisi digital, dimana X merepresentasikan jumlah bit yang error didalam sebuah pesan sepanjang n bit.
Distribusi Poisson
Sebuah r.v X disebut sebagai r.v poisson dengan parameter [latex]\alpha (> 0)[/latex] jika pmf-nya diberikan oleh
[latex]p_{x}(k)=P(X=k)=e^{-\alpha }\frac{\alpha ^{k}}{k!} \ \ \ \ \ \ \ \ k=0,1,2,…,n[/latex]
Fungsi distribusi (cdf) dari sebuah r.v poisson X adalah
[latex]F_{X}(x)=e^{-\alpha }\sum_{k=0}^{n} \frac{\alpha ^{k}}{k!} \ \ \ \ \ \ \ n\leq x\leq n+1[/latex]
Rata-rata dan varians dari r.v poission X adalah
[latex]\mu _{x}=\alpha \ \ \ dan \ \ \ \sigma _{X}^{2}[/latex]
Distribusi poisson dijumpai pada permasalahan-permasalahan yang melibatkan penghitungan cacah (counting) di dalam telekomunikasi, seperti memantau banyaknya permintaan sambungan telepon (atau panggilan telepon) di sebuah sentral telepon dalam suatu periode waktu tertentu. Distribusi Poisson berlaku pula pada permasalahan transmisi digital, jika data yang dikirimkan berjumlah besar sedangkan tingkat errornya kecil. Dalam kasus semacam ini, distribusi binomial sulit untuk digunakan sebagai piranti analitis. Akan tetapi, jika nilai rata-rata dari tingkat error berada dalam kisaran berhingga dan sama dengan [latex]\alpha[/latex], maka kita dapat menggunakan distribusi poisson sebagai taksiran pendekatan untuk distibusi normal.
Distribusi Normal atau Gaussian
Sebuah r.v X disebut sebagai r.v normal (Gaussian) jika pdf-nya ditentukan melalui rumusan :
[latex]f_{X}(x)=\frac{1}{\sqrt{2\pi \sigma }}e^{-\frac{(x-\mu )^2}{2\sigma ^2}}[/latex]
Fungsi distribusi (cdf) dari sebuah r.v normal atau gaussian X adalah :
[latex]F_{X}(x)=\frac{1}{\sqrt{2\pi \sigma }}\int_{-\infty }^{x}e^{-\frac{(\xi -\mu )^2}{2\sigma ^2}}d\xi =\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\frac{(x-\mu )}{\sigma }}e^{\frac{-\xi ^2}{2}}d\xi[/latex]
Integral pada persamaan di atas tidak dapat diselesaikan dengan batas-batas yang diberikan dan karenanya harus ditaksir dengan menggunakan metode numerik. Untuk memudakan pekerjaan ini, kita mendefinisikan sebuah fungsi Q(z) :
[latex]Q(z)=\frac{1}{\sqrt{2\pi}}\int_{z}^{\infty }e^{-\frac{\xi ^2}{2}}d\xi[/latex]
Sehingga, dapat dituliskan kembali menjadi :
[latex]F_{X}(x)=1-Q(\frac{x-\mu }{\sigma })[/latex]
Fungsi Q(z) dikenal sebagai fungsi error komplementer atau sekedar sebagai fungsi Q saja. Taksiran numerik nilai-nilai fungsi Q(z) dapat dilihat di dalam tabel fungsi komplementer.
Rata-rata dan varians dari random variabel normal (atau Gaussian) X adalah :
[latex]\mu _{x}=\mu \ \ \ dan \ \ \ \sigma _{X}^{2}=\sigma ^{2}[/latex]
kita akan menggunakan notasi [latex]N(\mu ;\sigma ^2)[/latex] untuk melambangkan r.v normal X dengan rata-rata [latex]\mu[/latex] dan varians [latex]\sigma ^2[/latex] . Secara khusus, [latex]N(0;1)[/latex] yaitu r.v normal X dengan rata-rata sebesar nol dan varians sebesar satu – mendefinisikan sebuah r.v normal baku.
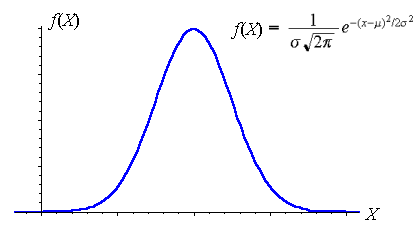
Distribusi normal (atau Gaussian) memainkan peranan penting di dalam berbagai kajian ilmu alam, khususnya yang berhubungan dengan fenomena-fenomena acak di alam. Banyak fenomena alamiah yang terjadi secara acak dapat ditaksir peluang kemunculannya sebagai sebuah distribusi normal. Alasan lainnya mengapa distribusi normal dianggap begitu penting adalah fakta yang diungkapkan oleh teorema limit-pusat (central-limit-theorem). Teorema ini menyatakan bahwa penjumlahan dari variabel-variabel acak yang sangat banyak, di bawah ini kondisi tertentu dapat ditaksir mendekati sebuah distribusi normal.
Referensi :
[2]. Komunikasi Analog dan Digital _ Hwei HSU