Kode konvolusi adalah kode linear yang memiliki struktur tambahan dalam generator matriks sehingga operasi pengkodean dapat dipandang sebagai filter ataupun operasi konvolusi. Dalam prakteknya kode konvolusi banyak diimplementasikan pada hardware yang di dalamnya tersedia encoding dan decoding. Konvolusi encoder merupakan sebuah filter digital linear, sistem time-invariant dengan urutan kode menjadi output interleaved dari output filter. Kode konvolusi banyak digunakan dalam prakteknya karena memberikan kinerja yang lebih baik dibandingkan dengan kode blok yang sebanding.
Kode konvolusi didefinisikan sebuah sistem kode yang memiliki bit informasi masukan harus lebih kecil daripada keluaran bit terkode dan yang paling penting kode konvolusi memiliki memori yang menyebabkan terciptanya sebuah aturan untuk mengkodekan setiap informasi bit masukan menjadi beberapa bit terkode berdasarkan bit-bit informasi masukan sebelumnya.
Kode konvolusi (n,k,m) merupakan satu set codeword dengan k input, n output dan m tingkat memori. Kode konvolusi ini dihasilkan dengan cara melewatkan urutan bit informasi melalui sejumlah tingkat shift register. Pada umumnya shift register terdiri dari N (k bit) tingkat dan m generator polynomial. Data masukan digeser sepanjang k bit shift register pada satu kali waktu. Jumlah bit keluaran untuk tiap k bit masukan n bit, dengan code rate R = k/n.
Parameter utama yang menjadi bagian utama dari convolutional code antara lain :
Rate
Merupakan rasio antara masukan bit informasi dengan keluaran bit terkode dan mempunyai persamaan sebagai berikut :
Keterangan :
R = Laju kode konvolusi
k = Jumlah bit masukan kode konvolusi
n = Jumlah bit keluaran kode konvolusi
Constraint Length
Jumlah delay elemen dalam kode konvolusi yaitu memori dengan masukan bit sekarang pada kode kovolusi atau dapat disebut juga panjang kode dari kode konvolusi. Constraint length dapat didefinisikan sebagai berikut :
Keterangan :
k = Constraint length
m = memori
Generator Polynomial
Generator polynomial sangat dibutuhkan untuk merangkai suatu kode konvolusi berdasarkan jumlah memori yang digunakan dalam suatu kode konvolusi selain itu setiap elemen pada generator polynomial serta jumlah dari generator polynomial mempengaruhi :
– Jumlah output
– Panjang kode konvolusi
– Hubungan antara shift register dan modul
Generator polynomial merupakan salah satu metode untuk menggambarkan matriks yang digunakan pada kode konvolusi. Generator polynomial ini biasanya ditulis dalam bentuk oktal. Setiap vektor pada matriks generator memiliki ukuran dimensi Kk dan mengandung garis hubungan pada encoder menuju modulo 2 adder. Masukan nilai “1” pada posisi I (baris) dari vektor untuk garis hubungan pada shift register yang menuju modulo 2 adder dengan masukan “0” pada posisi vector jika tidak ada hubungan antara shift register dengan modulo 2 adder [11] .
Encoder merupakan bagian kode konvolusi yang melakukan pengkodean data digital (berupa deret biner) yang diterima kode konvolusi sebelum ditransmisikan melalui saluran, sedangkan decoder kode konvolusi lebih rumit yang dimana biasanya menggunakan Viterbi Algorithm. Encoder kode konvolusi dengan panjang K = 3 dan rate ½
Terdapat dua tipe utama kode yang umum digunakan
- Kode Balok (Block Code)
- Kode Konvolusional (Convolutional Code)
Dengan kode balok (n,k) bit-bit data (informasi) dikelompokkan menjadi blok-blok sepanjang k bit, dan kemudian di sandikan untuk membentuk kode-kode biner (blok-blok kode) sepanjang n bit, di mana (n-k) bit yang ditambahkan ke bit-bit data aslinya berfungsi sebagai cek paritas. Salah satu karakteristik kodek balok linear adalah bahwa blok data k bit yang diumpankan ke enkoder pada saat tertentu secara langsung menentukan kode biner n bit yang akan dihasilkan oleh enkoder.
Di sisi lain, sebuah enkoder untuk kode konvolusional (n,k,m) juga menerima input berupa blok data k bit dan menghasilkan output berupa kode biner n bit. Namun berbeda halnya, pembentukan sebuah kode biner n bit tidak lagi hanya ditentukan oleh blok data k bit yang diumpankan sebelumnya. Sehingga, sebuah karakteristik penting dari kode konvolusional yang membedakannya dari kode balok biner adalah digunakannya memori di dalam proses penyandiannya. Dalam prakteknya, n maupun k adalah bilangan-bilangan bulat yang bernilai kecil dan tetap, sedangkan m akan diubah-ubah nilainya untuk mengatur redundansi pada kode.
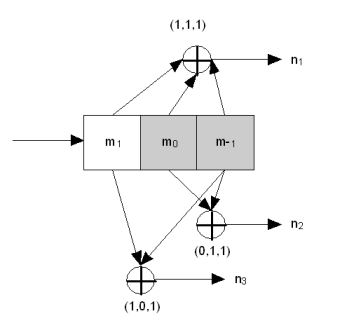
Bagan umum sebuah enkoder kode konvolusional (n,k,m) diperlihatkan pada gambar dibawah ini
Memperlihatkan enkoder dibentuk dari sebuah perangkat register geser (m x k) tahapan dan n buah penjumlah modulo-2. Di setiap satuan waktu, sebanyak k bit akan dimasukkan ke dalam k register tahap pertama, dan semua bit yang sudah ada sebelumnya di dalam register-register akan digeser sejauh k ke kanan, dan selanjutnya output dari penjumlah-penjumlah modulo-2 akan disampling secara berurutan untuk menghasilkan kode biner n bit.
Di dalam kasus khusus di mana k=1, rangkaian bit data tidak perlu dibagi terlebih dahulu menjadi blok-blok sepanjang k, dan dapat diolah terus-menerus secara berkesinambungan (kontinyu).
ENKODER KODE KONVOLUSIONAL
Kode-kode konvolusional sangat praktis, beberapa metode yang berbeda bahkan dapat digunakan untuk menjabarkan proses penyandian konvolusional, diantaranya, diagram koneksi, polinom koneksi, diagram keadaan (state diagram), diagram pohon (tree diagram) dan diagram trellis (trellis diagram).
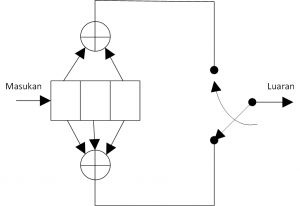
Gambar Sebuah enkoder konvolusional (2,1,3)
Pada gambar diatas, memperlihatkan sebuah enkoder konvolusional (2,1,3) sederhana dengan n=2,k=1 dan m=3. Setiap kali sebuah bit data dimasukkan ke register pertama pada enkoder, dua buah bit kode akan dihasilkan sebagai output secara berurutan.
Beberapa metode konvolusional
- Diagram Koneksi
- Polinomial
- State Diagram
- Tree Diagram
- Trellis Diagram
DECODER KODE KONVOLUSIONAL
-
Karakteristik Jarak untuk kode konvolusional
Jarak merupakan sebuah karakteristik penting bagi kode-kode konvolusional, yang menentukan kemampuan koreksi error dari kode yang bersangkutan. Parameter jarak terpenting bagi kode konvolusional adalah jarak bebas (free distance), yang dituliskan dengan notasi . Jarak bebas dari sebuah kode konvolusional didefinisikan sebagai jarak hamming minimum di antara dua kode biner di dalam himpunan kode konvolusional tersebut. Sebuah kode konvolusional dengan jarak bebas
akan mampu mengoreksi hingga t posisi error, jika dan hanya jika
Karena kode konvolusional adalah kode linear, juga merupakan bobot minimum dari kode-kode binernya yang dibangkitkan untuk blok-blook data bukan nol. Selain itu, jarak bebas adalah bobot minimum dari semua jalur yang keluar dari, dan berakhir di state nol di dalam diagram trellis. Sehingga,
dapat ditentukan dengan menggunakan diagram trellis untuk enkoder konvolusional yang membangkitkan kode yang bersangkutan.
2. Decoding Berbasis Kemungkinan Terbesar
Jika setiap blok data yang ada memiliki peluang kemunculan yang sama besar, maka sebuah dekoder yang memilih jika
di mana r adalah blok kode yang diterima di sisi penerima, dan adalah kode biner yang dibangkitkan dari salah satu blok data yang ada, dikenal dengan nama dekoder kemungkinan terbesar (maximum likelhood decoder). Besaran peluang kondisional
disebut sebagai fungsi kemungkinan (likelihood function). Perhatikan bahwa untuk sistem-sistem transmisi dengan kanal BSC (Binary Symmetric Channel), dekoder kemungkinan terbesar akan tersederhanakan menjadi dekoder jarak minimum. Prinsip decoding yang dijalankan oleh dekoder ini adalah sebagai berikut : Pilihlah
yang dapat meminimalkan jarak hamming di antara blok kode yang diterima r dan kode biner yang dikirimkan c.
3. Algoritma Decoding Viterbi
Prinsip decoding berbasis kemungkinan terbesar pada dasarnya bukan teknik praktis karena mengharuskan pencarian di seluruh ruang himpunan kode konvolusional untuk menemukan kode-kode biner tertentu, dan oleh sebab itu melibatkan komputasi yang sangat besar. Akan tetapi, sebuah algoritma decoding yang diciptakan oleh Viterbi dapat menerapkan prinsip decoding berbasis kemungkinan terbesar secara praktis, meski memang terbatas pada kode-kode konvolusional yang relatif pendek. Secara garis besar, decoding dilakukan dengan cara mencari sebuah jalur pada diagram trellis yang dapat menghasilkan kode biner output yang berjarak minimum ke blok kode yang diterima. Algoritma decoding Viterbi pada prinsipnya sama dengan teknik decoding berbasis jarak hamming minimum, namun beban komputasi di dalam proses dapat jauh direduksi dengan memanfaatkan struktur istimewa diagram trellis.
Memperhatikan diagram trellis dengan 4 state yang ada (a,b, c dan d) hanya dapat dicapai dari dua state lainnya. Sehingga, boleh jadi terdapat dua jalur yang berbeda yang menyatu di sebuah state yang sama, dan hanya jalur yang “paling cocok” dengan blok kode yang diterima perlu dipertahankan. Maka, algoritma viterbi pada dasarnya adalah permainan mencari jalur terpilih (survivor path) di tiap-tiap state pada diagram trellis, dimana terpilih disini berarti yang menghasilkan jarak minimum ke blok kode yang diterima r. Tiap-tiap garis transisi yang membentuk sebuah jalur terpilih akan mendapatkan nilai bobot atau metrik yang sama dengan jarak hammingnya ke segmen (pasangan bit) yang berpadanan pada blok kode yang diterima. Dengan menjumlahkan nilai-nilai bobot dari semua garis transisi pada sebuah jalur terpilih, kita mendapatkan metrik untuk jalur tersebut. Decoding kemudian dilakukan dengan memilih jalur terpilih yang memiliki metrik terkecil.
Lihat juga pembahasan tentang block code
Referensi
[1] Komunikasi Analog dan Digital _Hwei Hsu