Pada statistik jika kita ingin mengetahui distribusi dari suatu peubah acak kita bisa menggunakan mgf atau fungsi pembangkit momen. Selain itu kita juga bisa mencari ekspektasi dan variansi dari mgf ini.
[latex]\tiny \\ M(t)=E(e^{tX})\\ M(t)=e^{tX}\\ M'(0)=E[X]=\mu \\ M”(0)=E[X^2]\\ M^{(m)}(0)=E[X^m][/latex]
Peubah Acak Diskrit
[latex]\tiny \\ M(t)=E(e^{tX})=\sum_{x}^{}e^{tx}p(x) \\ M(t)=\sum_{x}^{}xe^{tx}p(x)[/latex]
[latex]\tiny \frac{de^{tx}}{dt}=xe^{tx}[/latex]
Bisa dimengerti ya pada momen turunan pertama, kedua dan selanjutnya kenapa jadi dikali .. karena diturunkan terhadap .. eksponensial kan kalau diturunkan konstanta dari variabelnya jadi dikalikan terhadap eksponensialnya. Hal yang sama berlaku untuk peubah acak yang kontinu.
Peubah Acak Kontinu
[latex]\tiny M(t)=E(e^{tX})=\int_{-\infty }^{\infty }e{tx}f(x)dx[/latex]
[latex]\tiny M'(t)=\frac{dM(t)}{dt}=\frac{d}{dt}\int_{-\infty }^{\infty }e^{tx}f(x)dx=\int_{-\infty }^{\infty }\frac{d}{dt}e^{tx}f(x)dx=\int_{-\infty }^{\infty }xe^{tx}f(x)dx[/latex]
[latex]\tiny M”(t)=\int_{-\infty }^{\infty }x^2e^{tx}f(x)dx[/latex]
Limiting Distribution MGF
Jika kita ingin mengetahui distribusi dari peubah acak selain dari melihat cdf peubah acak tersebut apa, kita dapat menggunakan mgf dengan cara limiting distribution… Untuk apa mengetahui distribusi suatu data? Untuk forecasting, untuk decision making atau untuk quality control.
Misal terdapat barisan peubah acak dan kita cari nilai mgf nya:
[latex]\tiny M_{x_{n}}(t)=E(e^{tX_{n}})[/latex]
Limit
[latex]\tiny \lim_{n \to \infty }M_{x_{n}}(t)=…[/latex]
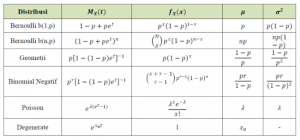
Lalu kita cocokkan dengan tabel dibawah merupakan fungsi yang seperti apa agar kita bisa tahu dia berdistribusi apa.
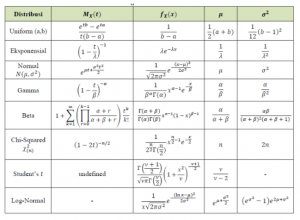
Tabel Distribusi Kontinu
Referensi :
[1] MonyetLogam_MGF